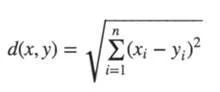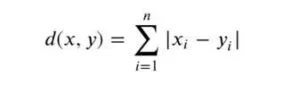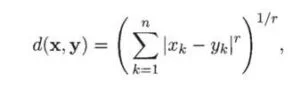K-Nearest Neighbors (KNN) Algorithm in Machine Learning: A Complete Guide

K-Nearest Neighbors (KNN), no, it’s not a new K-pop band group; it is actually one of the simplest supervised learning algorithms for machine learning.

Data analysis, along with pattern detection and prediction tasks, depend heavily on machine learning algorithms. Among various algorithms, K-Nearest Neighbors stands out due to its simplicity and effectiveness. It is widely used in classification and regression problems, making it a fundamental concept in machine learning.

This blog assesses K-Nearest Neighbors operations and its various business applications, as well as its advantages and weaknesses to help you recognize its central role in data-informed decision processes.

What is K-Nearest Neighbors (KNN)?

As a non-parametric lazy learning approach, K-Nearest Neighbors serves as an implementation algorithm for classification and regression execution.

The approach demonstrates versatility by not requiring any distribution assumption and provides simple implementation abilities. KNN operates by classifying new points using the common class found among their neighboring points in feature space. KNN determines regression values by averaging the numerical scores of neighboring points.

How KNN Works?

KNN follows a straightforward process:

• Choose the value of K– Nearest number of neighbors to be considered.
• Calculate the distance– We use different types of distance metrics

a) Euclidean: The shortest distance between two vectors is represented as the straight line connecting two data points in a plane. The following is the generalized formula for an n-dimensional space-; n=number of dimensions, (x_i,y_i) = data points

b) Manhattan: It is the total of all the absolute disparities between all the dimensions’ points. The following is the generalized formula for an n-dimensional space:

c) Minkowski: It is a generalized form of Euclidean and Manhattan distance; r= order of the norm

• Identify K nearest neighbors – Select the K closest points to the target data.
• Classify or predict – Assign a class label based on the majority of neighbors (for classification) or compute the average (for regression).

Choosing the Right K Value

The accuracy of the model depends on choosing an appropriate K value. A small K value results in overfitting since the model incorporates extraneous noise found in the dataset. Decisions become smoother when K increases while reducing the amount of variability. Most experts use cross-validation methods to identify the best K value.

Distance Metrics Used in KNN

Different distance measures serve as the basis of the algorithm when calculating the similarity of data points. Three major distance metrics are used in the algorithm: Euclidean Distance measures point through straight-line distances, and Euclidean Distance and Manhattan Distance are its main components. The distance calculation of Manhattan Distance consists of adding absolute dimension differences, and Minkowski Distance functions as a unified form of both Euclidean and Manhattan distances.

Applications of K-Nearest Neighbors

Various industries utilize K-Nearest Neighbors for its wide range of practical applications. The algorithm serves as a key component for image recognition systems involved in handwriting detection and face recognition duties. KNN functions as a key recommendation system tool to generate product suggestions based on user liking preferences. The algorithm performs medical diagnosis through data analysis of patient information to make disease diagnoses. Financial institutions use KNN to discover irregular money movements in their transactions.

Advantages of KNN:

• Simple Implementation
• Efficient on Small Datasets
• No Training Stage Required
• Versatility

The implementation of K-Nearest Neighbors remains straightforward because it requires low adjustment while yielding efficient outcomes from smaller data collections. The KNN system operates without demanding a training stage before it conducts predictions. The algorithm achieves flexibility through its ability to function as a predictor for both classification and regression needs.

Limitations of KNN

K-Nearest Neighbors presents both benefits and operational drawbacks to its users. When the dataset becomes larger the process of locating nearest neighbors becomes slower due to increasing computational complexity. The algorithm becomes highly reactive to noisy data since individual outliers can cause momentous changes to prediction results. The effectiveness of KNN decreases in high-dimensional data environments because sparsity affects its performance through the dimensionality curse.

Implementing Python of KNN Algorithm:

1. Library Importation:

To determine how many times an element appears in a list or iterable, use the counter function. After determining the labels of the k nearest neighbors in KNN, the Counter helps determine how frequently each label appears.

2. The Euclidean Distance Function Definition: 

To measure the Euclidean distance between points

3. Prediction Function for KNN:

The matching label (training_labels[i]) of the training data is associated with each distance.

This pair is kept in a distance list. The nearest points are at the top of the list since the distances are arranged in ascending order. The labels of the k nearest neighbors are then chosen by the algorithm.

The Counter class is used to count the labels of the k nearest neighbors, and the most common label is given back as the test_point prediction. The k neighbors’ majority vote served as the basis for this.

4. Test Point, Labels, and Training Data:

5. Prediction and Output:

Optimizing KNN for Better Performance

Several techniques enhance KNN’s efficiency. The normalization of datasets through Feature scaling makes distance metrics operate optimally. Efficiency in KNN improves accuracy through the usage of Principal Component Analysis (PCA) which reduces superfluous features. The implementation of KD-Trees and Ball Trees as advanced data structures allows KNN to execute nearest neighbor searches quickly when dealing with large datasets.

Summarizing the Key Points: 

K-Nearest Neighbors (KNN) operates as an effective basic machine learning tool. The success of KNN algorithms depends on both choosing the best K parameter and enhancing computation speed for better results. You can make use of KNN for different machine learning tasks when you examine its operational mechanisms together with its practical usage. It works effectively with dynamic datasets since it can make predictions without a training period.

However, issues like susceptibility to outliers and processing complexity must be taken into account. Even with its drawbacks, KNN is still a fundamental algorithm. KNN can be a useful tool in a data scientist’s toolbox, supporting precise forecasts and well-informed decision-making, provided that the parameters are tuned appropriately, and the advantages and disadvantages are carefully considered.

For more insights into machine learning and AI, visit YourTechDiet and explore our in-depth resources.